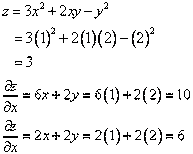
Partial Derivatives Crack+ Serial Number Full Torrent The difference quotient formula for finding the derivative of a function f(x) at a given x0 is D1(f)(x0) = f(x0+h) - f(x0) D2(f)(x0) = f(x0+h) - f(x0) where h is a small number. This produces values for the first derivative, D1(f)(x0), which are usually approximated using the central difference formula. In this example, we consider the function f(x) = x3 - x2 + x, for which the first derivative is D1(f)(x0) = 3x0 - 2x and the second derivative is D2(f)(x0) = 12x0 - 6x. The first-derivative value may be calculated using the central difference formula, D1(f)(x0) = f(x0 + h) - f(x0) = f(x0 + h) - (3x0 - 2x) = 3x0 - 2x + (3x0 - 2x) - 3x0 + 2x = -h (3x0 - 2x) + 0 = -h(3x0 - 2x) = -h(3x0 + 2x) = -h(6x0) = -h3x0 = -h3x0 + hx0 = -h3x0 + x0 = -h3x0 + x0 - hx0 = -hx0 (this is the correct value, as obtained by the derivative formula) and the second derivative is D2(f)(x0) = f(x0 + h) - f(x0) = (3x0 + 2x) - (3x0 - 2x) = 4x0 - 2x = 4x0 - 2x + h(4x0 - 2x) = h(4x0 - 2x) = h(4x0 + 2x) = h(12x0) = h(12x0) + hx0 = 12x0 - 2hx0 + x0 = 12x0 - 2hx0 + x0 - hx0 Partial Derivatives License Code & Keygen Free Download For PC [April-2022] ******************************************************* Choose one of the options below. 1) A simple application that find approximate numerical values for the 1st and 2nd order partial derivatives of a function at a given point. 2) A calculator that is used to define constants for your application. The user can choose which function he wants to use to find the derivative. The calculator can be used to define the constants he wants to use in his application. ***OPTION 1. A simple application that finds approximate numerical values for the 1st and 2nd order partial derivatives of a function at a given point. Choose the function you want to find the partial derivatives from the list of available functions below. After choosing a function you can click OK and your program will be ready. The result of your application is shown in the form of an image. Choose the tool of your choice to plot the images. The user can choose to save the images or print them. ***OPTION 2. A calculator that is used to define constants for your application. The user can choose the type of constants to be defined in the calculator. The user can define the constants to be used in the calculator. Before using the calculator the user must choose the variable to be used in the calculator. After the variable is selected the calculator appears. The user can define the values of the constants. After defining the constants the user can use the calculator to define the constants. The calculator will be ready for use. After using the calculator the user can use the results of his calculations by choosing the desired tool of his choice. The result of your application is shown in the form of an image. Choose the tool of your choice to plot the images. The user can choose to save the images or print them. ***OPTION 3. A help file with instructions, example and methodology. Choose the type of help you need. The help file will appear. ***OPTION 4. The application as a stand-alone tool. Choose the tool you want to use this as a stand-alone tool. The application will be shown. ***OPTION 5. The application with data. Choose the type of data you want to use. The data will be shown. Using the application: ******************************************************* Choose the option that you want to use. In the example the options are shown below. 1) The value of the function at the point you want to find the partial derivatives. 2) Your desired result. 3) A variable to store the result. 4) The tool of your choice to plot the images. 5) A variable to store 8e68912320 Partial Derivatives Download [32|64bit] [March-2022] [k] FIND FUNCTION POINTS The derivation of this function is trivial. Calculate the function value at a point [f] SAME FUNCTION AS USUAL EXCEPT [x] USER SPECIFIES THE FUNCTION, THE VALUE OF X IS SPECIFIED AS PART OF THE DESCRIPTION [f=X] FIND FUNCTION VALUE AT X The function value is calculated at an arbitrarily specified point. The point may be specified by a variable as follows: [x=X] USER SPECIFIES THE VALUE OF X [f=X] FIND FUNCTION VALUE AT X ... [n] FIND FUNCTION VALUE AT X Calculate the function value at a new point specified by the user, which may be specified by a variable as follows: [x=X] USER SPECIFIES THE VALUE OF X [f=X] FIND FUNCTION VALUE AT X ... [d] FIND FUNCTION VALUE AT X (PARTIAL DERIVATIVES) Calculate the 1st and 2nd order partial derivatives at a point specified by the user. [f=X] FIND FUNCTION VALUE AT X [p1=Y] USER SPECIFIES THE 1ST ORDER PARTIAL DERIVATIVE AT X [p2=Y] USER SPECIFIES THE 2ND ORDER PARTIAL DERIVATIVE AT X ... [x=X] USER SPECIFIES THE VALUE OF X [y=X] USER SPECIFIES THE VALUE OF Y [p1=X] USER SPECIFIES THE 1ST ORDER PARTIAL DERIVATIVE AT X [p2=X] USER SPECIFIES THE 2ND ORDER PARTIAL DERIVATIVE AT X ... [n] FIND FUNCTION VALUE AT X (PARTIAL DERIVATIVES) Calculate the 1st and 2nd order partial derivatives at a new point specified by the user. [f=X] FIND FUNCTION VALUE AT X [p1=X] USER SPECIFIES THE 1ST ORDER PARTIAL DERIVATIVE AT X [p2=X] USER SPECIFIES THE 2ND ORDER PARTIAL DERIVATIVE AT X What's New In Partial Derivatives? System Requirements: - Supported Windows platform: Windows 7 / 8 / 8.1 / 10 - Supported DirectX: DirectX 9.0c - Supported Processor: Intel i5-4690 2.66 GHz or above - Supported Graphic: NVIDIA GTX 1050 / AMD R9 270 2GB or above - Supported Resolution: 1920x1080, 2560x1440, 3840x2160 - Supported Graphics Memory: 4GB - Supported Hard Disk Space: 20 GB - Supported Sound Card: DirectX compatible sound card - Supported Keyboard
Related links:
Comments